experimental data acquisition
Immerse pH and reference
electrodes in a standard pH solution, ideally under temperature control and a
CO2-free atmosphere. Read the electric potential. Repeat this for at
least two more pH standard solutions. model prescription
The device known as a pH electrode
transduces H+ membrane potential to electric potential.
This is accomplished by coupling a H+-selective membrane with a Ag/AgCl electrochemical concentration cell; the basic scheme
is presented in Figure The general thermodynamic expression for
the chemical potential of a process with reaction quotient Q is shown in equation 1 where ΔG0 is the standard Gibbs energy for the
process, R is the ideal gas constant
and T is the temperature. If the
chemical process involves charge transfer then its chemical potential may be
expressed as an electric potential ΔE, equation 2, where F is the Faraday constant and n is the charge number of the ion, or
the number of moles of charges transferred per mole of the advancement of the
process. Substitution of equation 1 into equation 2 yields equation 3, known as
the Nernst equation, where ΔE0 is the standard potential. The observed
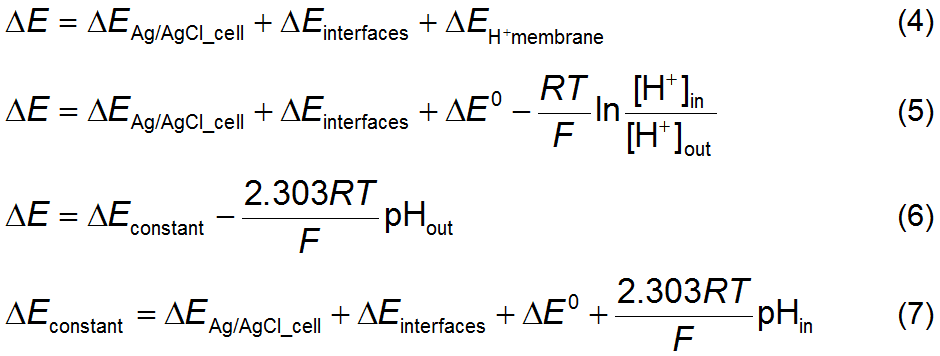
potential ΔE of a pH electrode is the sum of the series
of potentials shown in equation 4 where ΔEAg/AgCl_cell is the potential of the Ag/AgCl concentration cell and ΔEinterfaces is the
collective potential that develops at the several interfaces of the system due
to their asymmetries. Since the only potential that changes from one solution
to another is ΔEH+membrane then the observed potential
may be expressed by equation 5, using equation 3 to express ΔEH+membrane and
expanding Q to show the inner and
outer hydrogen ion concentrations. The use of concentrations instead of
activities is an approximation justified by its very low values. Since the
membrane is assumed to be H+-selective
then the measured potential is defined only by hydrogen ions. The value of n is +1 for the hydrogen cation. Changing the natural logarithms to decimal
logarithms, the electric potential measured by a pH electrode is described by
equation 6, where ΔEconstant is explained in equation 7.
Notice that this, temperature dependent, constant potential is the reference
potential against which the H+ potential is measured. Since equation
6 is linear on the parameters with variables E and pH, linear regression over these variables enables to
estimate the specific parameter values of the electrode and therefore to obtain
the quantitative relationship between potential and pH for an electrode. While
the y-intercept of equation 6, ΔEconstant, is electrode dependent, the
slope is theoretically defined as -2.303RT/F
and should be independent of the electrode. example and discussion
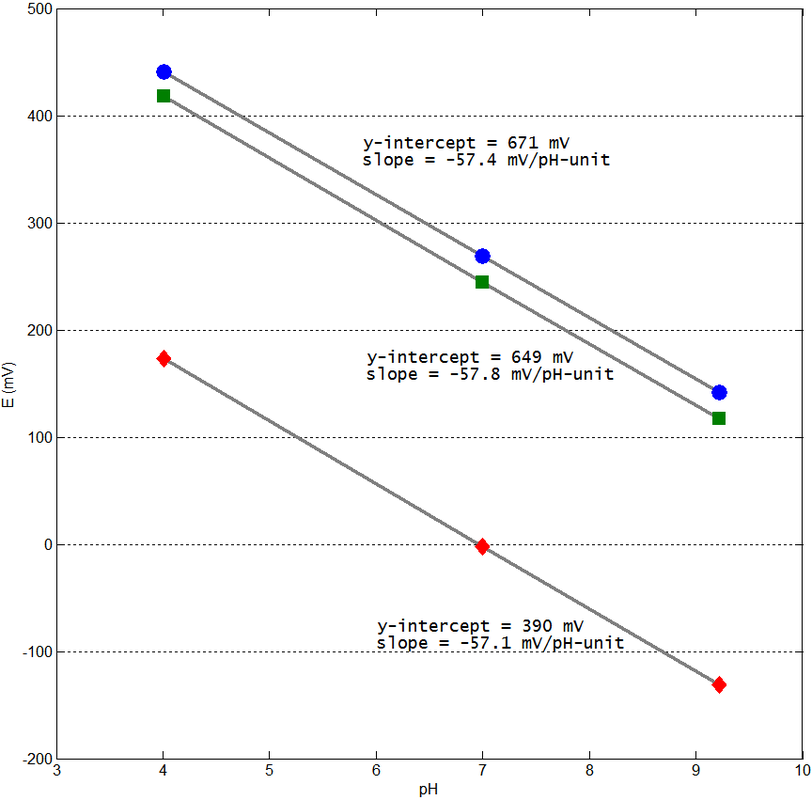
Figure 2 shows student
calibration results for three different pH electrodes. Three aspects about the
electrodes are evaluated after calibration: linearity of response, sensitivity
and asymmetry potential. Linearity of response is
a critical feature because it enables correct prediction of pH values using
equation 6. All three electrodes respond linearly and interpolation should be
very precise. However, care should be taken when extrapolating for more than
two pH units outside the extreme pH standards used. Calibrations were
performed at 298 K and so the slope is expected to have a value of -59.1
mV/pH-unit for all electrodes. The sensitivity of an electrode can be defined
as the ratio between the experimental slope and the theoretical slope and all
three electrodes perform near 97%, which is good. The experimental slope is a
measure of how strongly the electrode reacts to a pH difference between the two
sides of its membrane. A loss in sensitivity indicates some problem with the
electrode, or simply ageing, but if response linearity is maintained then pH
values are still correctly predicted by linear regression, although noise
instability will be noticeable. The asymmetry potential
is calculated, after calibration, as the potential for pH = 7. As can be seen
in Figure 2, the asymmetry potential may vary due to different Econstant values
because it depends on the specific values for the terms in equation 7. The
asymmetry potential changes if the inner electrode solutions change or the
porous junction of the reference electrode gets dirty, for example. Often, new
electrodes present approximately zero potential for pH = 7 (Figure 2, diamond
red markers) but that is not a necessary condition for good electrode
performance. references [1] http://www.coleparmer.com/TechLibraryArticle/560 |
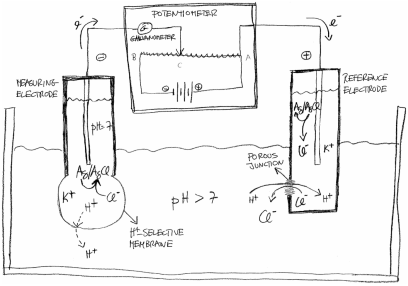
Figure 1 – Schematics of a potentiometric
pH measuring system, or pH-meter. It includes a measuring electrode, a
reference electrode and a potentiometer. The reference electrode closes the
electric circuit with an ion-permeable porous junction which also maintains the
neutrality of the solutions. Usually, the two electrodes are combined in one
piece where the reference electrode partially surrounds the measuring electrode. This is called a combined pH electrode but it is
normally referred to simply as pH electrode. Hydrogen ions may not actually
succeed in crossing the membrane beyond a superficial hydrated thin layer since
the potentiometer counteracts a net transport. Nevertheless, the in-out H+ concentration difference
is conveyed by ions in the inner dry glass.
|